新版 Ansys STK 13 Aviator 的重大升級與多節火箭發射模擬應用

Aviator 的核心升級：從航空到航太的跨域能力

新版 Ansys STK 對 Aviator 進行了跨代級更新，使其首次具備 從地面發射 → 亞軌道 → 進入軌道 的完整模擬能力，這也讓 STK 能更真實地支援多節火箭任務分析。

✦ 物理模型升級

• 全新重力與動力學模型，可處理 亞軌道 / 軌道飛行的連續轉換

• 最大速度上限提升至 8 km/s，足以模擬 LEO 入軌需求

• 支援更高動態壓力、跨音速與高超音速飛行條件

✦ 6-DOF（六自由度）飛行建模

STK 13.0 引入全新 6-DOF 控制框架，允許使用者自定義：

• 空氣動力模型（升力、阻力、力矩）

• 推進模型（多節火箭推力曲線、質量變化）

• 姿態控制邏輯（RCS、TVS、分離動作）

這些能力讓 多節火箭分離、翻轉、入軌點控制 的模擬變得可行且可視化。

Aviator 主要用於飛機和導彈的飛行模擬，並與其他 Ansys 工具（如 STK Astrogator）協同使用，以實現太空任務的整體分析

✦優點

• ‐多領域物理型分析能力強，能模擬包括熱、壓力、慣性等多種負載影響，貼近真實發射環境狀況。

• ‐具備可建立飛行性能模型的能力，能反映真實飛行操作與環境影響，如風勢和大氣效應，提供飛行路徑與操縱的精確模擬。

• ‐與STK其他功能整合，如軌跡規劃（Astrogator）、雷達模擬和通訊分析，進行全方位發射任務模擬，提高任務設計的準確性與全面性。

• ‐支援複雜操作模式，靈活決定模擬的複雜程度。

• ‐提供強大可視化與報告功能，能以3D動畫展示飛行軌跡和任務流程，便於分析分享。

✦由於Aviator功能強大，建議使用者相關背景

• ‐模型建立與操作複雜，建議有專業背景方能有效利用其多樣功能。

• ‐高度仿真模擬可能要求較長的計算資源與運算時間，特別是進行多物理場和多系統聯合模擬的時候。

• ‐初期學習曲線較陡峭，尤其是要掌握其程式自動化function 和API call (Matlab、Py、C#)。

對於太空運輸系統，STK(及Ansys)能夠提供的輔助包括

1️⃣ 液態火箭引擎與推進系統設

• Δv、推力、燃燒時間推算：Astrogator Segment 模型

‐Impulsive and Finite Thrust Models、 Thrust Vector、ISP…

‐STK Astrogator

• 熱環境資訊：STK Environment 模組

‐Solar Flux、Albedo、Eclipse…

‐星球重力場、大氣環境阻力與氣動力模型

‐Thermal Desktop + STK SEET (Space Environment and Effects Tool)

• 地球磁場 、銀河宇宙射線（Galactic Cosmic Rays, GCR）與太陽高能粒子（Solar Energetic Particles, SEP）模型

  

‐Fluent Aero + STK Aviator

• 分離事件分析

‐動畫與姿態追蹤 、CAD 模型匯入、整流罩內部空間配置可視化

• 火箭燃燒時機：Astrogator 自動求解

2️⃣ 結構與熱應力分析

‐Ansys Mechanical + Thermal Desktop + STK (熱分布可視化、場景模擬)

3️⃣衛星任務規劃和操作排程

‐STK Scheduler 對資源（例如衛星、感測器、地面站）的可用性和調度進行優化和分析

4️⃣通訊環境模擬

• 鏈路預算分析 (Link Budget Analysis): 模擬和分析從火箭（在飛行階段）到地面站（發射場或海面觀測船）之間的射頻 (RF) 通訊鏈路性能，評估訊號強度、損耗和潛在干擾。

• 覆蓋範圍與連通性分析 (Coverage and Connectivity Analysis): 確定在發射期間，火箭的飛行軌跡是否能持續與所需的地面接收站、追蹤雷達或其他通訊與追蹤站，建立持續可靠的連接，並分析通訊盲區。

• 干擾分析 (Interference Analysis): 透過模擬發射場外部的 RF 環境，評估多個發射器和接收器之間的潛在訊號干擾，確保關鍵通訊通道暢通無阻。

• 動態環境建模 (Dynamic Environment Modeling): STK 能夠在動態的物理模擬環境中，對火箭、地面站、天氣條件以及地形遮蔽等因素進行建模，以了解它們如何隨時間影響通訊效能。

關於多節火箭的一些小常識

Elon Musk(馬斯克)曾多次表示，如果地球的重力比現在多10%甚至20%，現有的化學火箭可能將無法使用，這是真的嗎?

 (摘錄自2019.07.21 https://www.cbsnews.com/news/extended-transcript-spacex-ceo-elon-musk-on-putting-boots-on-the-moon-and-mars/)

MUSK: Well, Wernher von Braun really knew what he was doing. I mean, his plans were for reusability. But those plans were stymied. I mean, it's so insane the way rockets work today with the exception of Falcon 9. It would be like if you got a plane and the way you get to your destination is you bail out with a parachute (LAUGHS) over the city in question and your plane crash lands somewhere. Okay, that's how rockets work today with the exception of Falcon 9. This is completely bonkers. It is so hard to make a rocket. It's about as hard to make a rocket as it is to make an advance airplane. Maybe rockets are a little harder in some ways. But not that much harder. it's just that we live in a deep gravity well. And so the technical difficulty of a fully reusable rocket is higher than the technical difficulty of a fully reusable plane. If Earth's gravity was just 10% lower fully reusable rockets would be easy.

And if it was 10% higher I think it might arguably be impossible. It's very finely balanced. So for example on Mars which has about 37% of Earth's gravity, you can go single stage, basically a single ship from the surface of Mars all the way to the surface of Earth. No booster required. But on Earth, you need a giant booster. Even though it's basically four tenths of the gravity. It's night and day

馬斯克： 嗯，Wernher von Braun（馮·布朗）真的很懂他在做什麼。我的意思是，他的設計本來就是為了可重複使用。但那些計畫後來被阻礙了。我的意思是，現在的火箭運作方式真的瘋狂，除了 Falcon 9 以外。這就好像你搭飛機時，抵達目的地的方式是——你在目標城市上空跳傘（笑），然後你的飛機在某個地方墜毀。好吧，這就是現在火箭的運作方式，除了 Falcon 9。這完全是瘋了。

製造火箭真的非常困難。做一枚火箭的難度大概跟製造一架先進的飛機差不多。也許火箭在某些方面更難，但也沒有難太多。只是我們生活在一個深重力井裡。因此，要做出一枚「完全可重複使用」的火箭，其技術難度比做出一架「完全可重複使用」的飛機還要高。如果地球的重力再低 10%，完全可重複使用的火箭就會變得容易。

而如果重力高 10%，我認為那可能就幾乎是不可能的。這是一個非常微妙的平衡。舉例來說，在火星上，重力大約是地球的 37%，你可以用單級火箭——基本上就是一艘船——從火星表面一路飛到地球表面，不需要助推器。但在地球上，你就需要一個巨大的助推器。即使火星的重力只有地球的大約四成，兩者之間仍然是天壤之別。

以下將嘗試以實際的計算，從運載火箭的燃料效率，的來了解一下為何馬斯克會說要做出一枚「完全可重複使用」的火箭是如此的困難。

何謂第一宇宙速度?

•        第一宇宙速度是指在地球上發射的物體繞地球飛行作圓周運動，使其再也不落回地球表面的最小初始速度。要作圓周運動，必須始終有一個力作用在太空飛行器上。其大小等於該太空飛行器運行線速度的平方乘以其質量再除以公轉半徑，即第一宇宙速度V₁ 。

•    

地球的重力加速度

•        令地球半徑R =6.378×10⁶m，地球質量M=5.97×10²⁴kg，萬有引力常數 G ≈ 6.67×10⁻¹¹ m³·kg⁻¹·s⁻² 代入並開根號，得V₁≈7.9公里/秒。

•        由於地球表面存在稠密的大氣層，太空飛行器受空氣阻力影響，不可能貼近地球表面作圓周運動，必須在約150公里的飛行高度上才能作圓周運動（在這高度的僅餘空氣阻力大致略去不計）。在此高度的環繞速度為7.8公里/秒。

比衝值 (Isp)

•        比衝值 (Isp) 就是推力除以燃料消耗率。Isp 越高，代表你用同樣的燃料可以產生更多推力。比衝量可以用兩種不同的單位來衡量：速度 (m/s) 或時間 (s)

•        速度很直觀，因為它代表火箭引擎的有效排氣速度。你的排氣速度越快，它每單位質量的推力就越大。

•        時間是一個不直觀的衡量單位，可能比較難以理解，但它的優點是，對每個人來說都完全一樣。你可以把 Isp (s) 想像成這個不切實際的物理問題的答案：「如果你的火箭只產生足夠的推力，讓 1 公斤的質量在海平面上懸停，它需要多久才能消耗 1 公斤的燃料？」

•        這是每單位燃料的衝量（動量變化），這變成: 力 x 時間 / 質量 = 質量 x 加速度 x 時間 / 質量，單位是 (公斤 米/秒²) x 秒 / 公斤，簡化後只剩下秒。

•        這兩個單位之間唯一的差別就是，你把速度 (m/s) 除以地球的重力 (m/s^2) 就可以得到時間 (s)。在火箭研發領域比較常用的是第二種，也就是時間 (s) 。相對而言，速度造成了一些問題，因為有些人用 m/s，而另一些人則用 ft/s。你甚至可以用 mph 或 kph 或 km/s，然後你真的會搞混。

•        美國在 1940 到 50 年代僱用了許多來自歐洲的火箭科學家，而且同時使用公制和英制是很困難的。所以當他們必須定義一個新的火箭效率度量時，他們選擇使用一個共同的單位，秒。這樣可以同時使用公制和英制，並且仍然得到相同單位的數字，以便他們可以相互比較火箭設計。新一代的火箭科學家確實改用了公制，這仍然是標準。

•        對於火箭來說，質量就是一切，而燃料是有質量的。你帶的燃料越多，你就能燃燒更多的燃料來產生推力。但是，你帶的燃料越多，你的火箭就越重，你的火箭越重，你就需要越多的速度。所以這是一個權衡。你希望帶最少的燃料，以到達你要去的地方。

運載火箭常用燃料(Methane、Kerosene...)與他們的比衝值

氧化劑(oxidizer)部分，液態氧是最為普遍使用，它不會主動溶解接觸物，可配合氫氣、甲烷、汽油、煤油、金屬等燃料。只要你添加適當的劑量，它們就會在燃燒室中愉快地燃燒。

至於燃料(fuels)部分，為何甲烷(Kerosene)是「折衷之選」？

一、效率 vs. 密度 (Trade-off)：

•        液氫(Liquid hydrogen)雖然比衝極高，但密度極低（需要巨大的油箱），且極低溫環境（-253°C）會導致金屬脆化及液氫洩漏。

•        煤油(Kerosene)密度最高，能讓火箭體積縮小，但在高壓引擎中容易產生「積碳」（Soot），阻礙引擎重複使用。

•        甲烷（-161°C）比衝比煤油高約 5%-10%，且燃燒極其乾淨，在 2025 年的重複使用火箭浪潮中（如 SpaceX 的星艦），成為平衡性能與營運成本的最佳選擇。

二、引擎設計的影響：比衝量不僅取決於燃料，也與引擎循環有關。例如 SpaceX 的 Raptor 引擎 採用了「全流量分級燃燒循環」（FFSC），使其能將甲烷的比衝推向理論極限（真空約 380s），甚至優於某些煤油引擎的理論表現。

推進劑組合	海平面比衝𝐼𝑠𝑝	真空比衝𝐼𝑠𝑝	典型代表引擎（型號）	主要優點(或缺點)
液態氫 / 液態氧 (LH2/LOX)	~360 - 390s	450 - 465s	RS-25 (SLS), RL10 (Centaur)	效率最高，排放僅有水蒸氣 體積極大、密度極低，需要超大型油箱，結構質量與火箭外形成本很高。 ​超低溫（約 20 K）造成嚴重滾沸損失與材料挑戰，需要複雜保溫與地面系統，不利長時間停泊或重複使用作業。
液態甲烷 / 液態氧 (LCH4/LOX)	~320 - 330s	370 - 385s	Raptor (Starship), BE-4 (Vulcan)	乾淨、無積碳，適合重複使用與火星上的燃料生產任務 比衝仍低於 LH₂/LOX，對極限任務（如上面級深空探測）在質量效率上略處劣勢。
煤油 / 液態氧 (RP-1/LOX)	~280 - 300s	320 - 350s	Merlin 1D (Falcon 9), RD-180 (Atlas V)	密度高、體積小，易於常溫儲存與大型推力設計 比衝較低，燃燒產生積碳與焦化，長時間或可重複使用發動機需頻繁檢修與清洗，也帶來額外污染排放。
肼類 / 四氧化二氮 (UDMH/N2O4)	~260 - 280s	300 - 330s	YF-20 (長征二號), 阿波羅服務艙	可在常溫長期儲存，具備自燃性，適合衛星姿態調整。 室溫儲存，密度高，系統可長期待命，非常適合戰略飛彈、長壽命衛星主推進與姿態控制。 劇毒且強腐蝕性，對地面人員與環境危害很大，安全與處置成本極高。
固體推進劑 (HTPB 等)	~240 - 260s	270 - 290s	SRB (SLS/太空梭助推器)	結構與系統簡單，燃料與氧化劑預先混合，不需複雜輸送管路與渦輪幫浦，可靠度高。 ​推力密度高，適合作為助推器或軍用飛彈，可長期儲存、快速發射，反應時間短。 無法中途關機或調整 比衝低，燃燒不均與燃燒不穩定（如振盪、侵蝕燃燒）設計與分析難度高。

燃料組合	噴射速度 ()	真空比衝 ()	能量密度與特性
液態氫 + 液態氧 (LH2/LOX)	~4,400 –  4,550 m/s	450 –  465 s	最快。分子量極小，排氣速度最高，但體積巨大。
液態甲烷 + 液態氧 (LCH4/LOX)	~3,600 –  3,750 m/s	370 –  385 s	中等。燃燒乾淨且效率高，是目前 2025 年新型火箭的首選。
煤油 + 液態氧 (RP-1/LOX)	~3,100 –  3,450 m/s	320 –  350 s	最慢。排氣分子較重，但密度高，適合火箭第一級大推力使用。

進入近地軌道（LEO）所需的Δ𝑉

•        燃氣噴射速度（Effective Exhaust Velocity, Ve）與比衝量（Isp）成正比關係

。這裡g0是一個定值，燃氣噴射速度則是由引擎本身的化學與熱力學特性決定的，與行星的質量或引力無關。因此酬載是否變少，需要從入軌速度與重力損失等角度來思考。

•        進入近地軌道（LEO）所需的Δ𝑉約為 9,400 m/s，這個數值並非單一公式的直接結果，而是由多個物理分量累積而成的「增量預算」（Delta-V Budget）。 

進入近地軌道（LEO）所需的Δ𝑉，計算方式可拆解為以下四個主要部分：

1. 軌道速度 (Orbital Velocity) —— 約 7,800 m/s 

•        這是進入軌道最核心的速度需求，即物體繞地球圓周運動而不掉落所需的橫向速度。 

•        計算公式 (軌道高度h，LEO 通常取 200–400 km)：

•        計算結果約為 7,800 m/s。 

2. 重力損失 (Gravity Drag) —— 約 1,200 - 1,500 m/s 

•        火箭在垂直上升階段，必須持續對抗地球引力。這段時間內引擎產生的部分推力被用來抵消重力，而非增加速度，這被視為一種速度損失。 

•        計算概念： 損失的大小取決於上升的時間與角度。公式近似為

•        對於一般火箭，這項損失約為 1,200–1,500 m/s。 

3. 空氣阻力與操縱損失 (Drag & Steering Loss) —— 約 300 - 500 m/s 

•        空氣阻力： 火箭穿越稠密大氣層時，空氣摩擦會消耗能量。

•        操縱損失： 火箭在執行「重力轉向」（Gravity Turn）改變飛行角度時產生的效率損失。

•        兩者合計通常約 300–500 m/s。 

4. 地球自轉補償 (Earth Rotation) —— 約 -400 m/s (省下) 

•        如果火箭向東發射，可以利用地球自轉的速度。 

•        在赤道附近向東發射，地球自轉可提供約 460 m/s 的初始速度，因此可以從總需求中減去這部分(相對的，如果是要發射光學衛星，一般選用繞極太陽同步軌道，這樣的話就會偏向南方發射)。 

5. 綜合計算總結 

•        將上述分量相加（考慮發射方向與損失）：

•        總 Δ𝑉≈7,800(軌道速度)+1,500(重力損失)+500(阻力)−400(自轉助推)≈𝟗,𝟒𝟎𝟎𝐦/𝐬

如果地球的重力比現在多10%甚至20%，酬載會變少嗎?

這是一個程序性作業問題，需要透過物理公式推導地球質量增加對火箭酬載的影響。

當地球質量 𝑀增加為 110%且半徑不變時，火箭的酬載比例會顯著下降，甚至可能導致現有單級火箭無法入軌。 

第一步：計算所需的增量速度(Δ𝑉) 變化

火箭進入軌道所需的總 Δ𝑉主要由第一宇宙速度（環繞速度）與重力損失組成： 

1. 環繞速度  

•        當𝑀變為1.1倍，新的速度 

•        原本約 7.8km/s的速度需增加約 380m/s

2.重力損失 Δ𝑉𝑔與地表重力 𝑔成正比

變為 1.1倍，重力損失也會增加約 10%（約增加 120m/s）。 

3. 總需求增加：原本進入近地軌道（LEO）約需 9,400m/s，在新環境下約需 9,900m/s (9400+380+120)

第二步：利用齊奧爾科夫斯基火箭方程計算質量比 

•      火箭方程為 

•        我們假設使用平均噴射速度 𝑣𝑒≈3,300m/s（煤油+液氧）： 

•      目前地球：

•      質量 110% 的地球：

•        這代表火箭燃燒後的剩餘總質量（包含結構與酬載）從5.79%降至4.98%

第三步：估算酬載比例的減損 

•        火箭的最終質量 由「結構質量」與「酬載質量」組成。假設現有火箭結構係數（乾重比）為 4%

•        目前酬載比例：5.79%−4%=𝟏.𝟕𝟗%

•        新環境酬載比例：4.98%−4%=𝟎.𝟗𝟖%

第四步：計算結果

•        如果地球質量增加為目前的 110%，現有火箭能夠攜帶的酬載比例將從約 1.79%，將大幅下降至約𝟎.𝟗𝟖% 。這意味著同樣一台火箭的運載能力將縮減約45%∼50%。 

•        以上的計算係假設各級火箭均不回收，如果執行回收任務時，火箭必須預留部分燃料用於著陸。以 2025 年的獵鷹 9 號為例，全回收模式下的酬載能力會從 22.8 噸降至約 17.5 噸。

燃氣噴射速度比較表 (真空環境) 

燃料組合	噴射速度 ()	真空比衝 ()	能量密度與特性
液態氫 + 液態氧 (LH2/LOX)	~4,400 - 4,550 m/s	450 - 465 s	最快。分子量極小，排氣速度最高，但體積巨大。
液態甲烷 + 液態氧 (LCH4/LOX)	~3,600 - 3,750 m/s	370 - 385 s	中等。燃燒乾淨且效率高，是目前 2025 年新型火箭的首選。
煤油 + 液態氧 (RP-1/LOX)	~3,100 - 3,450 m/s	320 - 350 s	最慢。排氣分子較重，但密度高，適合火箭第一級大推力使用。

多節火箭的數學基礎

對單一級火箭，使用齊奧爾科夫斯基火箭方程式：

若要用

的化學火箭達成 ，需要的質量比

 超過 10，幾乎無法兼顧結構強度與有效載荷。

多節火箭能夠達成 9,400 m/s 甚至更高的 Δv，核心原因是把「整體 Δv 需求」拆成數個較小 Δv、各階段各自擁有較溫和的質量比，並在燃燒結束後丟棄前一級的空重，使後續級不必背負「沒用的結構質量」。

對多節火箭，總 Δv 變成各級 Δv 的總和，例如三節火箭可寫成：

其中 是第 i 級的質量比，如此每一級只需達成較溫和的 ，但加總後仍可達到或超過 LEO 所需的 9.4 km/s。

「丟空重」如何重置質量比

多節火箭(staging)的關鍵操作是：

第 1 級燃燒結束時，火箭已接近第 1 級燃盡速度，並處於稀薄大氣或外太空。此時丟棄第 1 級的空油箱與引擎結構，使這些成為與火箭分離的「廢棄質量」。

接著由第 2 級點火，此時第 2 級的初始質量不再包含第 1 級的空重，質量比 因而大幅提升；同理，第 3 級相對於前兩級的空重也得到「重置」效應。​

從火箭方程式觀點看，每丟掉一級的空重，就相當於把「 很大、 也很大的單一級」拆成「多個 不那麼極端的子問題」，但所得到的 是加總起來的，因此總 Δv 比任一單級能達到的值大得多。

從 Δv 預算角度看 多節火箭 的必要性

典型地球表面到近地軌道的 Δv 預算約為 9.3–9.7 km/s（含重力損失與大氣阻力），單純 200–400 km 高度圓軌道的軌道速度約 7.8 km/s，其餘為損失。

單級化學火箭若要同時承受大氣阻力、重力損失、以及軌道插入，必須有遠高於實際材料與結構可承受的質量比與比衝。這就是為何多節火箭被視為達成 LEO 所需 Δv 的「必要技術」，而非單純的效率優化選項。

實際運載火箭的多節設計

現代大部分進入 LEO 的運載火箭（如獵鷹 9 號、長征系列、Ariane、Atlas、Soyuz）均採二級或三級設計，甚至再加上上面級，用於更高能量任務（例如 GEO、月球或行星際轉移）。

這些火箭的共同特徵包括：

下級設計成高推重比、適應高動壓的大氣層飛行；

上級設計成高比衝、在近真空環境中工作；

各級燃盡後立即分離，以最大化後續級可用的質量比與 Δv，使總 Δv 達到 LEO 甚至更高軌道或離軌任務需求。

如果地球半徑不變，但質量增加為目前的110%，現有火箭能夠攜帶的酬載比例會變為多少?

終於來到最開始由馬斯克提出的問題了(揮汗…)。對於這個問題，需要透過物理公式推導地球質量增加對火箭酬載的影響。

當地球質量 𝑀增加為 110%且半徑不變時，火箭的酬載比例會顯著下降，甚至可能導致現有單級火箭無法入軌。 

第一步：計算所需的增量速度(Δ𝑉) 變化 

火箭進入軌道所需的總 Δ𝑉主要由第一宇宙速度（環繞速度）與重力損失組成： 

1. 環繞速度 

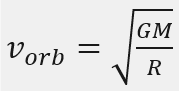
當𝑀變為1.1倍，新的速度

原本約 7.8km/s的速度，需增加約 380m/s

2. 重力損失 Δ𝑉𝑔與地表重力 𝑔成正比

   

變為 1.1倍，重力損失也會增加約 10%（約增加 120m/s）。

3. 總需求增加：原本進入近地軌道（LEO）約需 9,400m/s，在新環境下約需 9,900m/s (9400+380+120)

第二步：利用齊奧爾科夫斯基火箭方程計算質量比 

火箭方程為 

我們假設使用平均噴射速度𝑣𝑒≈3,300m/s（煤油+液氧）： 

1. 目前地球：

   

2. 質量 110% 的地球：

這代表火箭燃燒後的剩餘總質量（包含結構與酬載）從5.79%降至4.98%

第三步：估算酬載比例的減損 

火箭的最終質量 由「結構質量」與「酬載質量」組成。假設現有火箭結構係數（乾重比）為 4%

• 目前酬載比例：5.79%−4%=𝟏.𝟕𝟗%

• 新環境酬載比例：4.98%−4%=𝟎.𝟗𝟖%

第四步：答案 

• 如果地球質量增加為目前的 110%，現有火箭能夠攜帶的酬載比例將從約 1.79%，將大幅下降至約𝟎.𝟗𝟖% 。這意味著同樣一台火箭的運載能力將縮減約45%∼50%。

• 以上的計算係假設各級火箭均不予回收，如果執行回收任務時，火箭必須預留部分燃料用於著陸。以 2025 年的獵鷹 9 號為例，全回收模式下的酬載能力會從 22.8 噸降至約 17.5 噸。因此，若是真的地球的地心引力再向上提升，火箭的回收任務勢必更為不可行。

參考資料

2019.07.21: Extended transcript: SpaceX CEO Elon Musk on putting boots on the moon and Mars

https://www.cbsnews.com/news/extended-transcript-spacex-ceo-elon-musk-on-putting-boots-on-the-moon-and-mars/

2025.11.01: Elon Musk explains to Joe Rogan why Earth’s gravity makes launching rockets such an incredible engineering challenge. They discuss the immense energy and precision required to overcome gravity’s pull and reach orbit — and how SpaceX designs its rockets to make this process more efficient. Musk breaks down the physics behind rocket launches and why escaping Earth is much harder than most people think.

超精簡版https://www.youtube.com/shorts/I9QZVqXvQIs

稍微長一點版https://youtu.be/1BywUie9uJg

原版Joe Rogan Experience #2404 - Elon Musk

(超過三小時) https://youtu.be/O4wBUysNe2k